GBA三作的实际命中率研究
对于GBA三作的乱数有基本了解的人都知道,命中的判定需要消耗2个乱数,而不是我们所想象中的一个;而且也有很多人对于命中率做过测试,结果也都表明战斗信息窗口中显示的命中率与实际命中的频率存在着不可忽略的偏差。看来这个偏差应该是由于2乱数判定命中所造成的。
首先定义一下后面将要用到的2个名词:
理论命中率:战斗信息窗口中显示的命中率
实际命中率:实际战斗中命中的概率
注:原则上讲命中率应该是介于0~1之间的一个数值,这里为了便于大家的直观理解以及方便和乱数进行统一,叙述中常常提到的2个词为理论命中和实际命中,它们和游戏中显示的一样,为0~100之间的数值。
下面将介绍Alucard所采用的测试方法:
1.确定在命中的判定中使用的2个乱数的具体数值
已知圣魔中狙击手的“必的”特技判定是战斗中使用的第一个乱数,那么通过不断修改狙击手等级的方法就可以确切知道这第一个乱数的具体数值(比如30级的狙击手没发动“必的”,而31级发动,那么乱数就是30);连续运用此方法可以依次测试出所需用到的全部乱数。
2.测试2乱数如何判定命中率
当我们知道了判定命中时所使用的乱数的具体数值后,通过修改角色的能力来调整理论命中值,直到找到一个临界命中值(比如理论命中为78时攻击命中,77时为攻击miss,那么77就是我们要找的临界命中值),然后通过临界命中值与乱数的比较后,发现临界命中值等于2个乱数的平均值!
因此2乱数判定命中的方法为:
如果 理论命中>(乱数1+乱数2)/2,那么判定攻击命中;反之判定攻击miss。
注:除法的小数部分会舍去。
以上是Alucard的测试所得出的结论,下面对这个结果进行一下分析。
令average=(乱数1+乱数2)/2
通常来讲我们可以认为乱数是服从均匀分布的,也就是说乱数的值为0~99的概率都相等,为1%,模拟产生10000个乱数,其分布大致如下:
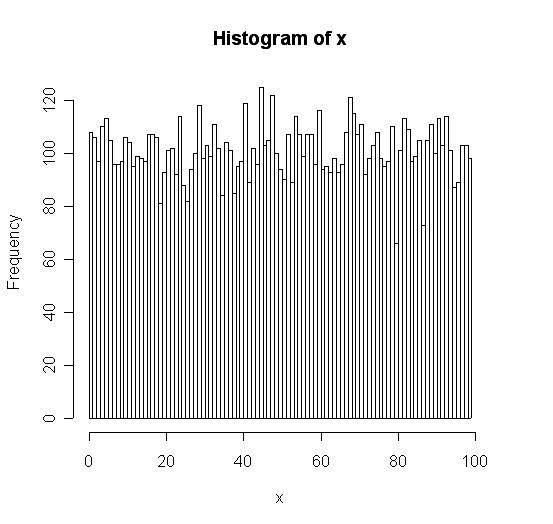
而对2个这样的乱数取了均值之后,直观的想象也会知道它的数值更容易在50左右,再分别模拟产生2组10000个乱数,取其均值,分布情况大致如下:
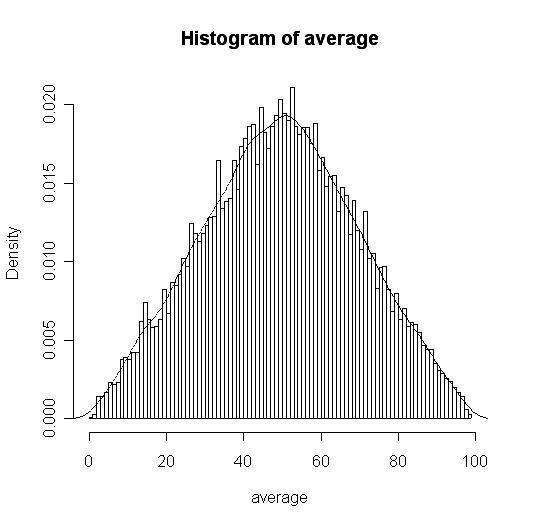
可以很清楚的看到两种极端的数值很少出现,之后总结出实际命中的判定公式为(数学推导略^_^):
实际命中=x*(2x+1)/100
(x<=50)
实际命中=100-(100-x)*(199-2x)/100
(x>50)
式子中,x为理论命中,取值0~100
实际命中,取值0~100
当然一个数学式子看起来肯定会令多数人感到郁闷,所以下面干脆总结了一个理论命中率与实际命中率对应的表,同时进行了2组模拟:第三列是通过程序生成的伪随机数模拟了1000万次,给出了对应实际命中的频率;第四列则是从GBA的乱数表中取出连续的10000个乱数进行测试,给出了对应实际命中的频率,这两列模拟值也供大家参考:
| 理论命中率 |
实际命中率 |
程序模拟测试 |
乱数表测试 |
| 0% |
0% |
0% |
0% |
| 1% |
0.03% |
0.03074% |
0.04% |
| 2% |
0.10% |
0.10137% |
0.13% |
| 3% |
0.21% |
0.21045% |
0.20% |
| 4% |
0.36% |
0.36178% |
0.40% |
| 5% |
0.55% |
0.55251% |
0.54% |
| 6% |
0.78% |
0.78231% |
0.78% |
| 7% |
1.05% |
1.05589% |
1.05% |
| 8% |
1.36% |
1.36706% |
1.25% |
| 9% |
1.71% |
1.71892% |
1.57% |
| 10% |
2.10% |
2.11155% |
1.93% |
| 11% |
2.53% |
2.54281% |
2.38% |
| 12% |
3.00% |
3.01256% |
2.73% |
| 13% |
3.51% |
3.51983% |
3.27% |
| 14% |
4.06% |
4.07097% |
3.79% |
| 15% |
4.65% |
4.66434% |
4.13% |
| 16% |
5.28% |
5.29018% |
4.66% |
| 17% |
5.95% |
5.95889% |
5.29% |
| 18% |
6.66% |
6.66737% |
6.08% |
| 19% |
7.41% |
7.42156% |
6.76% |
| 20% |
8.20% |
8.21108% |
7.62% |
| 21% |
9.03% |
9.04155% |
8.29% |
| 22% |
9.90% |
9.91503% |
9.16% |
| 23% |
10.81% |
10.82690% |
10.07% |
| 24% |
11.76% |
11.77852% |
11.16% |
| 25% |
12.75% |
12.77024% |
12.12% |
| 26% |
13.78% |
13.79873% |
13.25% |
| 27% |
14.85% |
14.86698% |
14.23% |
| 28% |
15.96% |
15.98334% |
15.31% |
| 29% |
17.11% |
17.13541% |
16.48% |
| 30% |
18.30% |
18.32901% |
17.48% |
| 31% |
19.53% |
19.56181% |
18.87% |
| 32% |
20.80% |
20.83595% |
20.22% |
| 33% |
22.11% |
22.15153% |
21.50% |
| 34% |
23.46% |
23.49983% |
22.91% |
| 35% |
24.85% |
24.89771% |
24.21% |
| 36% |
26.28% |
26.33326% |
25.87% |
| 37% |
27.75% |
27.80115% |
27.55% |
| 38% |
29.26% |
29.30989% |
29.05% |
| 39% |
30.81% |
30.86392% |
30.53% |
| 40% |
32.40% |
32.45801% |
32.06% |
| 41% |
34.03% |
34.09230% |
33.82% |
| 42% |
35.70% |
35.76993% |
35.44% |
| 43% |
37.41% |
37.47713% |
37.08% |
| 44% |
39.16% |
39.22865% |
38.74% |
| 45% |
40.95% |
41.02162% |
40.52% |
| 46% |
42.78% |
42.84880% |
42.45% |
| 47% |
44.65% |
44.71423% |
44.16% |
| 48% |
46.56% |
46.62824% |
46.21% |
| 49% |
48.51% |
48.58414% |
48.26% |
| 50% |
50.50% |
50.56887% |
50.00% |
| 51% |
52.47% |
52.53738% |
52.01% |
| 52% |
54.40% |
54.47051% |
53.96% |
| 53% |
56.29% |
56.36575% |
55.95% |
| 54% |
58.14% |
58.21923% |
57.88% |
| 55% |
59.95% |
60.02256% |
59.79% |
| 56% |
61.72% |
61.79352% |
61.49% |
| 57% |
63.45% |
63.51847% |
63.22% |
| 58% |
65.14% |
65.21020% |
64.81% |
| 59% |
66.79% |
66.86027% |
66.42% |
| 60% |
68.40% |
68.46948% |
67.97% |
| 61% |
69.97% |
70.03801% |
69.47% |
| 62% |
71.50% |
71.56699% |
71.22% |
| 63% |
72.99% |
73.05266% |
72.59% |
| 64% |
74.44% |
74.49712% |
74.05% |
| 65% |
75.85% |
75.90488% |
75.41% |
| 66% |
77.22% |
77.26939% |
76.88% |
| 67% |
78.55% |
78.60344% |
78.23% |
| 68% |
79.84% |
79.88986% |
79.52% |
| 69% |
81.09% |
81.13782% |
80.68% |
| 70% |
82.30% |
82.34741% |
81.90% |
| 71% |
83.47% |
83.51864% |
83.13% |
| 72% |
84.60% |
84.65131% |
84.07% |
| 73% |
85.69% |
85.73382% |
85.16% |
| 74% |
86.74% |
86.78381% |
86.22% |
| 75% |
87.75% |
87.79143% |
87.44% |
| 76% |
88.72% |
88.75977% |
88.25% |
| 77% |
89.65% |
89.68472% |
89.26% |
| 78% |
90.54% |
90.56693% |
90.24% |
| 79% |
91.39% |
91.41762% |
90.99% |
| 80% |
92.20% |
92.22597% |
91.83% |
| 81% |
92.97% |
92.98957% |
92.62% |
| 82% |
93.70% |
93.71731% |
93.40% |
| 83% |
94.39% |
94.41074% |
94.03% |
| 84% |
95.04% |
95.05420% |
94.71% |
| 85% |
95.65% |
95.66271% |
95.49% |
| 86% |
96.22% |
96.23342% |
96.07% |
| 87% |
96.75% |
96.75933% |
96.67% |
| 88% |
97.24% |
97.24914% |
97.25% |
| 89% |
97.69% |
97.69771% |
97.72% |
| 90% |
98.10% |
98.10408% |
98.12% |
| 91% |
98.47% |
98.47311% |
98.42% |
| 92% |
98.80% |
98.80415% |
98.85% |
| 93% |
99.09% |
99.09257% |
99.15% |
| 94% |
99.34% |
99.33952% |
99.31% |
| 95% |
99.55% |
99.05033% |
99.53% |
| 96% |
99.72% |
99.71970% |
99.75% |
| 97% |
99.85% |
99.84892% |
99.90% |
| 98% |
99.94% |
99.93941% |
99.96% |
| 99% |
99.99% |
99.98996% |
99.99% |
| 100% |
100% |
100% |
100% |
之后个人利用通信斗技场进行模拟战,在77的命中率下攻击200次,命中183次,miss17次,命中频率为91.5%,和表中推算出的89.65%的实际命中率大致相符(有兴趣的朋友也可以做做测试,看看和推算值是否相符)。
最后对这个2乱数判定命中进行一下总结,从公式或是上面的对应表中,我们可以发现理论命中高于50时,其实际命中会高于理论值(比如理论命中率为70%,实际命中率却高达82.3%);而当理论命中低于50时则正好相反,实际命中会低于理论值。在实际战斗当中,我们所遇到的多数情况是,我方的理论命中高于50,而敌方的理论命中低于50,从而导致我方的实际命中更高,敌方的实际命中更低。因此2乱数判定命中的最终效果就是以一种不易为我们所觉察的方式来降低游戏的难度。


 火花天龙剑 -> 火炎之纹章 -> 精华区 -> GBA三作的实际命中率研究
火花天龙剑 -> 火炎之纹章 -> 精华区 -> GBA三作的实际命中率研究

